TL;DR

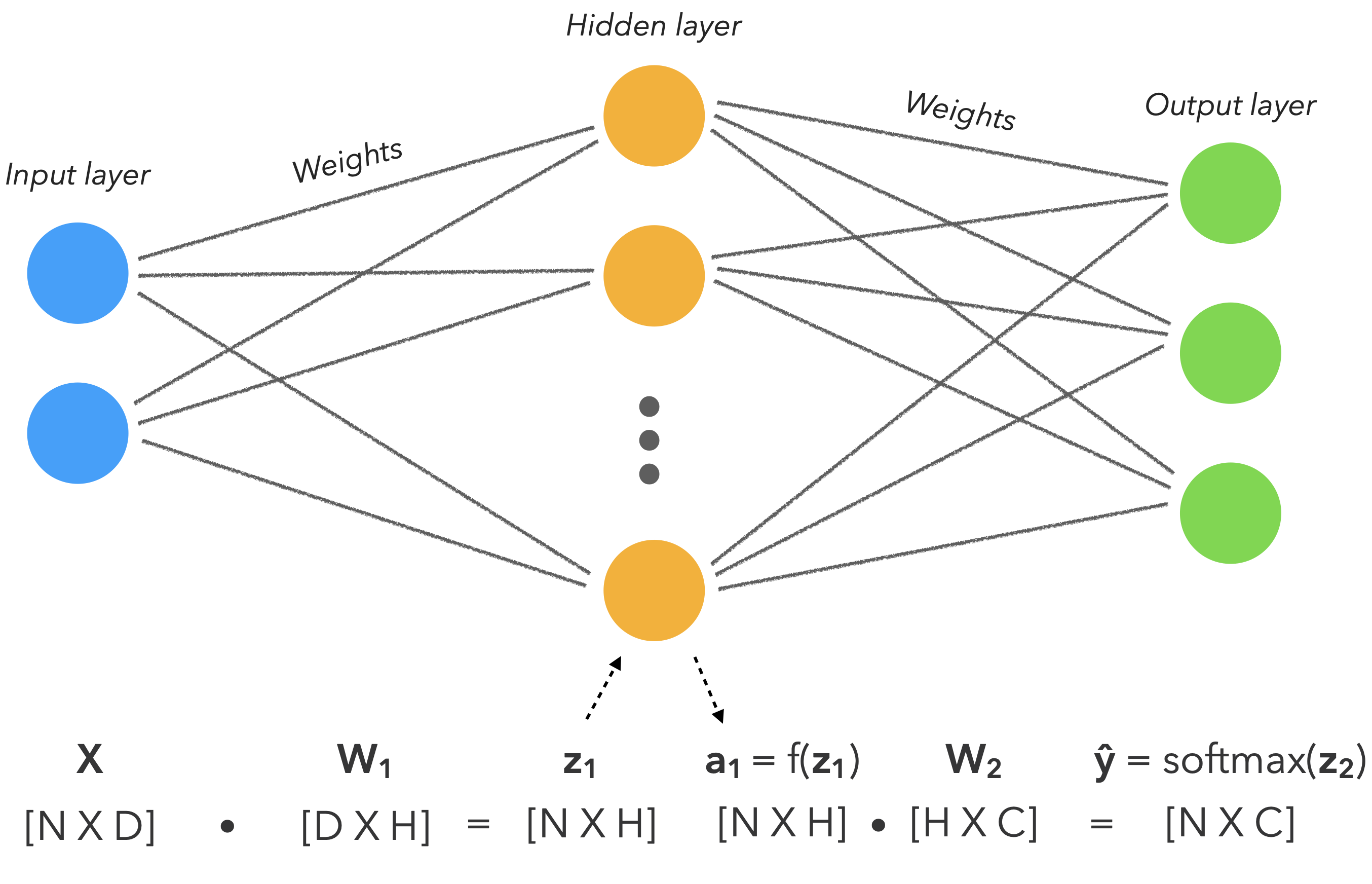
本章的目标依然是学习一种模型 $\hat{y}$，能准确对输入 $X$ 及对应的输出 $y$ 进行建模。

你会注意到神经网络只是我们迄今为止看到的广义线性方法的扩展，但具有非线性激活函数，因为我们的数据是高度非线性的。

$$
z_1 = XW_1
$$

$$
a_1 = f(z_1)
$$

$$
z_2 = a_1W_2
$$

$$
\hat{y} = softmax(x)
$$

参数 解释
$N$ 样本数
$D$ 特征数
$H$ 隐藏神经元
$C$ 标签数
$W_1$ 第一层的权重
$z_1$ 第一层的输出
$f$ 非线性激活函数
$a_1$ 第一层的激活值
$W_2$ 第二层的权重
$z_2$ 第二层的输出

Set up

1
2
3
4
5
6
7
8
import numpy as np
import random

SEED = 1024

# Set seed for reproducibility
np.random.seed(SEED)
random.seed(SEED)

Load data

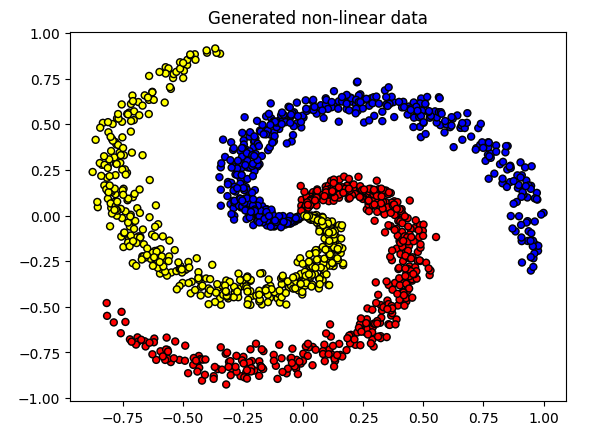
这里准备了一份非线性可分的螺旋数据来学习。

1
2
3
4
5
6
7
8
import matplotlib.pyplot as plt
import pandas as pd

# Load data
url = "http://s3.mindex.xyz/datasets/9378f64fc8dd2817e4c92be0a3bae8e7.csv"
df = pd.read_csv(url, header=0) # load
df = df.sample(frac=1).reset_index(drop=True) # shuffle
df.head()

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# Data shapes
X = df[["X1", "X2"]].values
y = df["color"].values
print ("X: ", np.shape(X))
print ("y: ", np.shape(y))

# Output
# X:  (1500, 2)
# y:  (1500,)

# Visualize data
plt.title("Generated non-linear data")
colors = {"c1": "red", "c2": "yellow", "c3": "blue"}
plt.scatter(X[:, 0], X[:, 1], c=[colors[_y] for _y in y], edgecolors="k", s=25)
plt.show()

Split data

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
import collections
from sklearn.model_selection import train_test_split

TRAIN_SIZE = 0.7
VAL_SIZE = 0.15
TEST_SIZE = 0.15

def train_val_test_split(X, y, train_size):
    X_train, X_, y_train, y_ = train_test_split(X, y, train_size=TRAIN_SIZE, stratify=y)
    X_test, X_val, y_test, y_val = train_test_split(X_, y_, train_size=0.5, stratify=y_)
    return X_train, X_val, X_test, y_train, y_val, y_test

# Create data splits
X_train, X_val, X_test, y_train, y_val, y_test = train_val_test_split(
    X=X, y=y, train_size=TRAIN_SIZE)
print (f"X_train: {X_train.shape}, y_train: {y_train.shape}")
print (f"X_val: {X_val.shape}, y_val: {y_val.shape}")
print (f"X_test: {X_test.shape}, y_test: {y_test.shape}")
print (f"Sample point: {X_train[0]} → {y_train[0]}")

# Output
# X_train: (1050, 2), y_train: (1050,)
# X_val: (225, 2), y_val: (225,)
# X_test: (225, 2), y_test: (225,)
# Sample point: [0.17003003 0.63079261] → c3

Label encoding

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
from sklearn.preprocessing import LabelEncoder

# Output vectorizer
label_encoder = LabelEncoder()

# FIt on train date
label_encoder = label_encoder.fit(y_train)
classes = list(label_encoder.classes_)
print(f"classes: {classes}")

# Output
# classes: ['c1', 'c2', 'c3']


# Convert labels to tokens
print (f"y_train[0]: {y_train[0]}")
y_train = label_encoder.transform(y_train)
y_val = label_encoder.transform(y_val)
y_test = label_encoder.transform(y_test)
print (f"y_train[0]: {y_train[0]}")

# Output
# y_train[0]: c3
# y_train[0]: 2


# Class weights
counts = np.bincount(y_train)
class_weights = {i: 1.0/count for i, count in enumerate(counts)}
print (f"counts: {counts}\nweights: {class_weights}")

# Output
# counts: [350 350 350]
# weights: {0: 0.002857142857142857, 1: 0.002857142857142857, 2: 0.002857142857142857}

Standardize data

因为 $y$ 是类别值，所以我们只标准化 $X$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
from sklearn.preprocessing import StandardScaler

# Standardize the data (mean=0, std=1) using training data
X_scaler = StandardScaler().fit(X_train)

# Apply scaler on training and test data (don't standardize outputs for classification)
X_train = X_scaler.transform(X_train)
X_val = X_scaler.transform(X_val)
X_test = X_scaler.transform(X_test)

# Check (means should be ~0 and std should be ~1)
print (f"X_test[0]: mean: {np.mean(X_test[:, 0], axis=0):.1f}, std: {np.std(X_test[:, 0], axis=0):.1f}")
print (f"X_test[1]: mean: {np.mean(X_test[:, 1], axis=0):.1f}, std: {np.std(X_test[:, 1], axis=0):.1f}")

# Output
# X_test[0]: mean: 0.0, std: 1.0
# X_test[1]: mean: -0.0, std: 1.0

Linear model

在尝试使用神经网络之前，为了解释激活函数，我们先用前面学到的逻辑回归模型来学习我们的数据。

你会发现一个用线性激活函数的线性模型对我们的数据来说并不是合适的。

Model & Train

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
import torch

from torch import nn
import torch.nn.functional as F

from torch.optim import Adam


INPUT_DIM = X_train.shape[1] # X is 2-dimensional
HIDDEN_DIM = 100
NUM_CLASSES = len(classes) # 3 classes

class LinearModel(nn.Module):
    def __init__(self, input_dim, hidden_dim, num_classes):
        super(LinearModel, self).__init__()
        self.fc1 = nn.Linear(input_dim, hidden_dim)
        self.fc2 = nn.Linear(hidden_dim, num_classes)

    def forward(self, x_in):
        z = self.fc1(x_in) # linear activation
        z = self.fc2(z)
        return z

# Initialize model
model = LinearModel(input_dim=INPUT_DIM, hidden_dim=HIDDEN_DIM, num_classes=NUM_CLASSES)

LEARNING_RATE = 1e-2
NUM_EPOCHS = 10
BATCH_SIZE = 32

class_weights_tensor = torch.Tensor(list(class_weights.values()))
loss_fn = nn.CrossEntropyLoss(weight=class_weights_tensor)

# Accuracy
def accuracy_fn(y_pred, y_true):
    n_correct = torch.eq(y_pred, y_true).sum().item()
    accuracy = (n_correct / len(y_pred)) * 100
    return accuracy

# Optimizer
optimizer = Adam(model.parameters(), lr=LEARNING_RATE)

# Convert data to tensors
X_train = torch.Tensor(X_train)
y_train = torch.LongTensor(y_train)
X_val = torch.Tensor(X_val)
y_val = torch.LongTensor(y_val)
X_test = torch.Tensor(X_test)
y_test = torch.LongTensor(y_test)

# Training
for epoch in range(NUM_EPOCHS):
    # Forward pass
    y_pred = model(X_train)

    # Loss
    loss = loss_fn(y_pred, y_train)

    # Zero all gradients
    optimizer.zero_grad()

    # Backward pass
    loss.backward()

    # Update weights
    optimizer.step()

    if epoch%1==0:
        predictions = y_pred.max(dim=1)[1] # class
        accuracy = accuracy_fn(y_pred=predictions, y_true=y_train)
        print (f"Epoch: {epoch} | loss: {loss:.2f}, accuracy: {accuracy:.1f}")


# Output
# Epoch: 0 | loss: 1.18, accuracy: 43.7
# Epoch: 1 | loss: 0.92, accuracy: 55.6
# Epoch: 2 | loss: 0.79, accuracy: 54.5
# Epoch: 3 | loss: 0.74, accuracy: 54.4
# Epoch: 4 | loss: 0.73, accuracy: 53.9
# Epoch: 5 | loss: 0.73, accuracy: 53.9
# Epoch: 6 | loss: 0.74, accuracy: 55.0
# Epoch: 7 | loss: 0.75, accuracy: 55.8
# Epoch: 8 | loss: 0.76, accuracy: 56.2
# Epoch: 9 | loss: 0.77, accuracy: 56.7

Evaluation

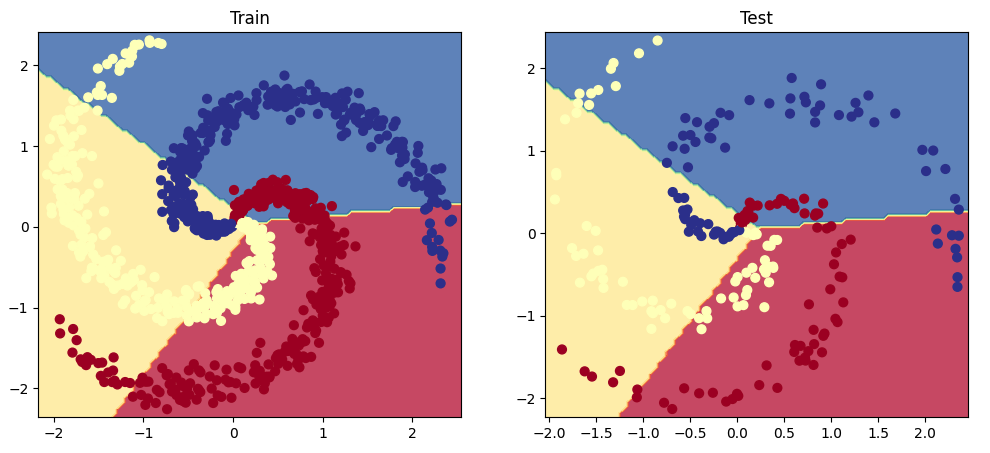
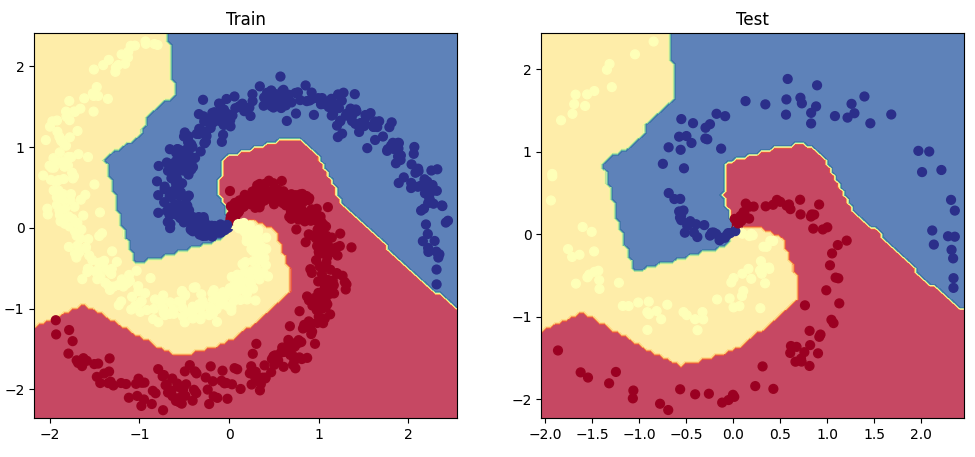
我们来看一下这个线性模型在螺旋数据上的表现如何。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
import json
import matplotlib.pyplot as plt
from sklearn.metrics import precision_recall_fscore_support


def get_metrics(y_true, y_pred, classes):
    """Per-class performance metrics."""
    # Performance
    performance = {"overall": {}, "class": {}}

    # Overall performance
    metrics = precision_recall_fscore_support(y_true, y_pred, average="weighted")
    performance["overall"]["precision"] = metrics[0]
    performance["overall"]["recall"] = metrics[1]
    performance["overall"]["f1"] = metrics[2]
    performance["overall"]["num_samples"] = np.float64(len(y_true))

    # Per-class performance
    metrics = precision_recall_fscore_support(y_true, y_pred, average=None)
    for i in range(len(classes)):
        performance["class"][classes[i]] = {
            "precision": metrics[0][i],
            "recall": metrics[1][i],
            "f1": metrics[2][i],
            "num_samples": np.float64(metrics[3][i]),
        }

    return performance

# Predictions
y_prob = F.softmax(model(X_test), dim=1)
print (f"sample probability: {y_prob[0]}")
y_pred = y_prob.max(dim=1)[1]
print (f"sample class: {y_pred[0]}")

# Output
# sample probability: tensor([0.3424, 0.0918, 0.5659], grad_fn=<SelectBackward0>)
# sample class: 2

# Performance
performance = get_metrics(y_true=y_test, y_pred=y_pred, classes=classes)
print (json.dumps(performance, indent=2))

# Output
# {
#   "overall": {
#     "precision": 0.5174825174825175,
#     "recall": 0.5155555555555555,
#     "f1": 0.5162093875662788,
#     "num_samples": 225.0
#   },
#   "class": {
#     "c1": {
#       "precision": 0.5194805194805194,
#       "recall": 0.5333333333333333,
#       "f1": 0.5263157894736841,
#       "num_samples": 75.0
#     },
#     "c2": {
#       "precision": 0.46153846153846156,
#       "recall": 0.48,
#       "f1": 0.47058823529411764,
#       "num_samples": 75.0
#     },
#     "c3": {
#       "precision": 0.5714285714285714,
#       "recall": 0.5333333333333333,
#       "f1": 0.5517241379310344,
#       "num_samples": 75.0
#     }
#   }
# }


def plot_multiclass_decision_boundary(model, X, y):
    x_min, x_max = X[:, 0].min() - 0.1, X[:, 0].max() + 0.1
    y_min, y_max = X[:, 1].min() - 0.1, X[:, 1].max() + 0.1
    xx, yy = np.meshgrid(np.linspace(x_min, x_max, 101), np.linspace(y_min, y_max, 101))
    cmap = plt.cm.Spectral

    X_test = torch.from_numpy(np.c_[xx.ravel(), yy.ravel()]).float()
    y_pred = F.softmax(model(X_test), dim=1)
    _, y_pred = y_pred.max(dim=1)
    y_pred = y_pred.reshape(xx.shape)
    plt.contourf(xx, yy, y_pred, cmap=plt.cm.Spectral, alpha=0.8)
    plt.scatter(X[:, 0], X[:, 1], c=y, s=40, cmap=plt.cm.RdYlBu)
    plt.xlim(xx.min(), xx.max())
    plt.ylim(yy.min(), yy.max())

# Visualize the decision boundary
plt.figure(figsize=(12,5))
plt.subplot(1, 2, 1)
plt.title("Train")
plot_multiclass_decision_boundary(model=model, X=X_train, y=y_train)
plt.subplot(1, 2, 2)
plt.title("Test")
plot_multiclass_decision_boundary(model=model, X=X_test, y=y_test)
plt.show()

Activation functions

使用广义的线性方法产生了较差的结果，因为我们试图用线性激活函数去学习非线性数据。

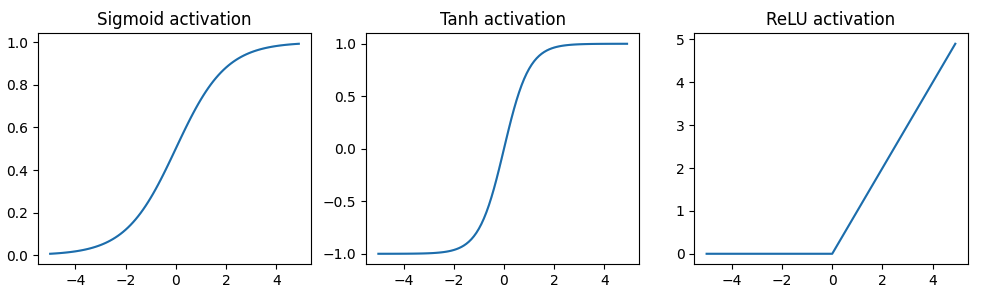
所以我们需要一个可以能让模型学习到数据中的非线性的激活函数。有几种不同的选择，我们稍微探索一下。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
# Fig size
plt.figure(figsize=(12,3))

# Data
x = torch.arange(-5., 5., 0.1)

# Sigmoid activation (constrain a value between 0 and 1.)
plt.subplot(1, 3, 1)
plt.title("Sigmoid activation")
y = torch.sigmoid(x)
plt.plot(x.numpy(), y.numpy())

# Tanh activation (constrain a value between -1 and 1.)
plt.subplot(1, 3, 2)
y = torch.tanh(x)
plt.title("Tanh activation")
plt.plot(x.numpy(), y.numpy())

# Relu (clip the negative values to 0)
plt.subplot(1, 3, 3)
y = F.relu(x)
plt.title("ReLU activation")
plt.plot(x.numpy(), y.numpy())

# Show plots
plt.show()

ReLU激活函数$(max(0, z))$ 是目前为止用的最广泛的激活函数。但每个激活函数都有自己适用场景。比如：如果我们需要输出在0和1之间，那么sigmoid是合适的选择。

*（在某些情况下，ReLU函数也是不够的。例如，当神经元的输出大多为负时，激活函数的输出为0，这将导致神经元“死去”。为了减轻这种影响，我们可以降低学习率活着使用“ReLU变种”。 如 Leaky ReLU 或 PRelu，它们会适当倾斜于神经元的负输出。）

NumPy

现在，我们创建一个与逻辑回归模型完全相似的多层感知机，但包含一个学习数据中非线性的激活函数。

Initialize weights

第一步: 随机初始化模型的权重$W$。（后面会介绍更有效的初始化策略）

1
2
3
4
5
6
7
8
9
# Initialize first layer's weights
W1 = 0.01 * np.random.randn(INPUT_DIM, HIDDEN_DIM)
b1 = np.zeros((1, HIDDEN_DIM))
print (f"W1: {W1.shape}")
print (f"b1: {b1.shape}")

# Output
# W1: (2, 100)
# b1: (1, 100)

Model

第二步: 讲输入 $X$ 送到模型中进行前向传播以得到网络的输出。

首先，我们将输入传给第一层。
$$
z_1 = XW_1
$$

1
2
3
4
5
6
# z1 = [NX2] · [2X100] + [1X100] = [NX100]
z1 = np.dot(X_train, W1) + b1
print (f"z1: {z1.shape}")

# Output
# z1: (1050, 100)

接下来，我们应用非线性激活函数Relu。
$$
a_1 = f(z_1)
$$

1
2
3
4
5
6
# Apply activation function
a1 = np.maximum(0, z1) # ReLU
print (f"a_1: {a1.shape}")

# Output
# a_1: (1050, 100)

然着我们将激活函数的输出传给第二层，以获得logit。
$$
z_2 = a_1W_2
$$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
# Initialize second layer's weights
W2 = 0.01 * np.random.randn(HIDDEN_DIM, NUM_CLASSES)
b2 = np.zeros((1, NUM_CLASSES))
print (f"W2: {W2.shape}")
print (f"b2: {b2.shape}")

# Output
# W2: (100, 3)
# b2: (1, 3)

# z2 = logits = [NX100] · [100X3] + [1X3] = [NX3]
logits = np.dot(a1, W2) + b2
print (f"logits: {logits.shape}")
print (f"sample: {logits[0]}")

# Output
# logits: (1050, 3)
# sample: [ 0.00017606 -0.0023457   0.00035913]

之后，我们将应用softmax来获得网络的概率输出。

$$
\hat{y} = softmax(z_2)
$$

1
2
3
4
5
6
7
8
9
10
# Normalization via softmax to obtain class probabilities
exp_logits = np.exp(logits)
y_hat = exp_logits / np.sum(exp_logits, axis=1, keepdims=True)
print (f"y_hat: {y_hat.shape}")
print (f"sample: {y_hat[0]}")

# Output
# y_hat: (1050, 3)
# sample: [0.33359304 0.33275285 0.33365411]

Loss

第三步： 利用交叉熵计算我们分类任务的损失。
$$
J(\theta) = - \sum_i^K{log(\hat{y}_i)} = - \sum_i^K{log(\frac{e^{W_yX_i}}{\sum_j{e^{WX_i}}})}\\
$$

1
2
3
4
5
6
7
# Loss
correct_class_logprobs = -np.log(y_hat[range(len(y_hat)), y_train])
loss = np.sum(correct_class_logprobs) / len(y_train)
print (f"loss: {loss:.2f}")

# Output
# loss: 1.10

Gradients

第四步 计算损失函数 $J(\theta)$ 相对于权重的梯度。

对于$W_2$的梯度，与前篇逻辑回归的梯度相同，因为 $\hat{y} = softmax(z_2)$

$$
\begin{split}
\frac{\partial{J}}{\partial{W_{2j}}} &= \frac{\partial{J}}{\partial{\hat{y}}} \frac{\partial{\hat{y}}}{\partial{W_{2j}}} \\
&= - \frac{1}{\hat{y}} \frac{\partial{\hat{y}}}{\partial{W_{2j}}} \\
&= - \frac{1}{\frac{e^{a_1 W_{2y}}}{\sum_j{e^{a_1 W}}}} \frac{\sum_j{e^{a_1 W}e^{a_1 W_{2y}} 0 - e^{a_1 W_{2y}} e^{a_1 W_{2j}} a_1 }}{(\sum_j{e^{a_1 W}})^2} \\
&= \frac{a_1 e^{a_1 W_{2j}}}{\sum_j{e^{a_1 W}}} \\
&= a_1 \hat{y}
\end{split}
$$

$$
\begin{split}
\frac{\partial{J}}{\partial{W_{2y}}} &= \frac{\partial{J}}{\partial{\hat{y}}} \frac{\partial{\hat{y}}}{\partial{W_{2y}}} \\
&= - \frac{1}{\hat{y}} \frac{\partial{\hat{y}}}{\partial{W_{2y}}} \\
&= - \frac{1}{\frac{e^{a_1 W_{2y}}}{\sum_j{e^{a_1 W}}}} \frac{\sum_j{e^{a_1 W}e^{a_1 W_{2y}} a_1 - e^{W_{2y} a_1}e^{a_1 W_{2y}} a_1}}{(\sum_j{e^{a_1 W}})^2} = \frac{1}{\hat{y}} (a_1 \hat{y}^2 - a_1 \hat{y}) \\
&= a_1 (\hat{y} - 1)
\end{split}
$$

对于 $W_1$ 的梯度计算有点棘手，因为我们必须要通过两组权重进行反向传播。

$$
\begin{split}
\frac{\partial{J}}{\partial{W_1}} &= \frac{\partial{J}}{\partial{\hat{y}}} \frac{\partial{\hat{y}}}{\partial{X}} \frac{\partial{X}}{\partial{z_1}} \frac{\partial{z_1}}{\partial{W_1}} \\
&= W_2 (\partial{\hat{y}})(\partial{ReLU})X
\end{split}
$$

1
2
3
4
5
6
7
8
9
10
11
12
# dJ/dW2
dscores = y_hat
dscores[range(len(y_hat)), y_train] -= 1
dscores /= len(y_train)
dW2 = np.dot(a1.T, dscores)
db2 = np.sum(dscores, axis=0, keepdims=True)

# dJ/dW1
dhidden = np.dot(dscores, W2.T)
dhidden[a1 <= 0] = 0 # ReLu backprop
dW1 = np.dot(X_train.T, dhidden)
db1 = np.sum(dhidden, axis=0, keepdims=True)

Update weights

第五步 指定一个学习率来更新权重 $W$，惩罚错误的分类奖励正确的分类。
$$
W_i = W_i - \alpha \frac{\partial{J}}{\partial{W_i}}
$$

1
2
3
4
5
# Update weights
W1 += -LEARNING_RATE * dW1
b1 += -LEARNING_RATE * db1
W2 += -LEARNING_RATE * dW2
b2 += -LEARNING_RATE * db2

Training

第六步: 重复步骤 2 ~ 5，以最小化损失为目的来训练模型

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
# Convert tensors to NumPy arrays
X_train = X_train.numpy()
y_train = y_train.numpy()
X_val = X_val.numpy()
y_val = y_val.numpy()
X_test = X_test.numpy()
y_test = y_test.numpy()

# Initialize random weights
W1 = 0.01 * np.random.randn(INPUT_DIM, HIDDEN_DIM)
b1 = np.zeros((1, HIDDEN_DIM))
W2 = 0.01 * np.random.randn(HIDDEN_DIM, NUM_CLASSES)
b2 = np.zeros((1, NUM_CLASSES))

# Training loop
for epoch_num in range(1000):

    # First layer forward pass [NX2] · [2X100] = [NX100]
    z1 = np.dot(X_train, W1) + b1

    # Apply activation function
    a1 = np.maximum(0, z1) # ReLU

    # z2 = logits = [NX100] · [100X3] = [NX3]
    logits = np.dot(a1, W2) + b2

    # Normalization via softmax to obtain class probabilities
    exp_logits = np.exp(logits)
    y_hat = exp_logits / np.sum(exp_logits, axis=1, keepdims=True)

    # Loss
    correct_class_logprobs = -np.log(y_hat[range(len(y_hat)), y_train])
    loss = np.sum(correct_class_logprobs) / len(y_train)

    # show progress
    if epoch_num%100 == 0:
        # Accuracy
        y_pred = np.argmax(logits, axis=1)
        accuracy =  np.mean(np.equal(y_train, y_pred))
        print (f"Epoch: {epoch_num}, loss: {loss:.3f}, accuracy: {accuracy:.3f}")

    # dJ/dW2
    dscores = y_hat
    dscores[range(len(y_hat)), y_train] -= 1
    dscores /= len(y_train)
    dW2 = np.dot(a1.T, dscores)
    db2 = np.sum(dscores, axis=0, keepdims=True)

    # dJ/dW1
    dhidden = np.dot(dscores, W2.T)
    dhidden[a1 <= 0] = 0 # ReLu backprop
    dW1 = np.dot(X_train.T, dhidden)
    db1 = np.sum(dhidden, axis=0, keepdims=True)

    # Update weights
    W1 += -1e0 * dW1
    b1 += -1e0 * db1
    W2 += -1e0 * dW2
    b2 += -1e0 * db2

# Output
# Epoch: 0, loss: 1.098, accuracy: 0.519
# Epoch: 100, loss: 0.541, accuracy: 0.680
# Epoch: 200, loss: 0.305, accuracy: 0.893
# Epoch: 300, loss: 0.135, accuracy: 0.951
# Epoch: 400, loss: 0.091, accuracy: 0.976
# Epoch: 500, loss: 0.069, accuracy: 0.984
# Epoch: 600, loss: 0.056, accuracy: 0.989
# Epoch: 700, loss: 0.048, accuracy: 0.991
# Epoch: 800, loss: 0.043, accuracy: 0.994
# Epoch: 900, loss: 0.039, accuracy: 0.994

Evaluation

在测试集上评估这个模型。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
class MLPFromScratch():
    def predict(self, x):
        z1 = np.dot(x, W1) + b1
        a1 = np.maximum(0, z1)
        logits = np.dot(a1, W2) + b2
        exp_logits = np.exp(logits)
        y_hat = exp_logits / np.sum(exp_logits, axis=1, keepdims=True)
        return y_hat

# Evaluation
model = MLPFromScratch()
y_prob = model.predict(X_test)
y_pred = np.argmax(y_prob, axis=1)

# # Performance
performance = get_metrics(y_true=y_test, y_pred=y_pred, classes=classes)
print (json.dumps(performance, indent=2))

# Output
# {
#   "overall": {
#     "precision": 0.9826749826749827,
#     "recall": 0.9822222222222222,
#     "f1": 0.9822481383871041,
#     "num_samples": 225.0
#   },
#   "class": {
#     "c1": {
#       "precision": 1.0,
#       "recall": 0.9733333333333334,
#       "f1": 0.9864864864864865,
#       "num_samples": 75.0
#     },
#     "c2": {
#       "precision": 0.9615384615384616,
#       "recall": 1.0,
#       "f1": 0.9803921568627451,
#       "num_samples": 75.0
#     },
#     "c3": {
#       "precision": 0.9864864864864865,
#       "recall": 0.9733333333333334,
#       "f1": 0.9798657718120806,
#       "num_samples": 75.0
#     }
#   }
# }

def plot_multiclass_decision_boundary_numpy(model, X, y, savefig_fp=None):
    """Plot the multiclass decision boundary for a model that accepts 2D inputs.
    Credit: https://cs231n.github.io/neural-networks-case-study/

    Arguments:
        model {function} -- trained model with function model.predict(x_in).
        X {numpy.ndarray} -- 2D inputs with shape (N, 2).
        y {numpy.ndarray} -- 1D outputs with shape (N,).
    """
    # Axis boundaries
    x_min, x_max = X[:, 0].min() - 0.1, X[:, 0].max() + 0.1
    y_min, y_max = X[:, 1].min() - 0.1, X[:, 1].max() + 0.1
    xx, yy = np.meshgrid(np.linspace(x_min, x_max, 101),
                         np.linspace(y_min, y_max, 101))

    # Create predictions
    x_in = np.c_[xx.ravel(), yy.ravel()]
    y_pred = model.predict(x_in)
    y_pred = np.argmax(y_pred, axis=1).reshape(xx.shape)

    # Plot decision boundary
    plt.contourf(xx, yy, y_pred, cmap=plt.cm.Spectral, alpha=0.8)
    plt.scatter(X[:, 0], X[:, 1], c=y, s=40, cmap=plt.cm.RdYlBu)
    plt.xlim(xx.min(), xx.max())
    plt.ylim(yy.min(), yy.max())

    # Plot
    if savefig_fp:
        plt.savefig(savefig_fp, format="png")

# Visualize the decision boundary
plt.figure(figsize=(12,5))
plt.subplot(1, 2, 1)
plt.title("Train")
plot_multiclass_decision_boundary_numpy(model=model, X=X_train, y=y_train)
plt.subplot(1, 2, 2)
plt.title("Test")
plot_multiclass_decision_boundary_numpy(model=model, X=X_test, y=y_test)
plt.show()

Ending

神经网络是机器学习和人工智能领域的基础，我们必须彻底掌握。

Citation

1
2
3
4
5
6
@article{madewithml,
    author       = {Goku Mohandas},
    title        = { Neural networks - Made With ML },
    howpublished = {\url{https://madewithml.com/}},
    year         = {2022}
}