TL;DR

Way2AI系列，确保出发去"改变世界"之前，我们已经打下了一个坚实的基础。

本文的目标是使用NumPy实现一个多项式逻辑回归模型 $\hat{y}$ ，以实现对给定的特征$X$预测其目标类别的概率分布。

$$
\hat{y} = \frac{e^{XW_y}}{\sum_j{e^{XW}}}
$$

逻辑回归与前篇所述的线性回归，同属于广义线性回归。皆是建模一条直线(或一个平面)。但不同的是，逻辑回归是一种分类模型。

Set up

1
2
3
4
5
6
7
8
import numpy as np
import random

SEED = 1024

# Set seed for reproducibility
np.random.seed(SEED)
random.seed(SEED)

Load data

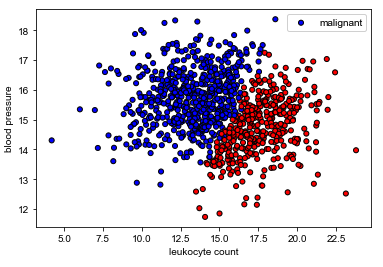
我们的任务是基于白细胞计数和血压来确定肿瘤是否为良性（无害）或恶性（有害）。

请注意，这是一个合成数据集，没有临床意义。

1
2
3
4
5
6
7
8
9
import matplotlib.pyplot as plt
import pandas as pd
from pandas.plotting import scatter_matrix

# Read from CSV to Pandas DataFrame
url = "http://s3.mindex.xyz/datasets/tumors.csv"
df = pd.read_csv(url, header=0) # load
df = df.sample(frac=1).reset_index(drop=True) # shuffle
df.head()

1
2
3
4
5
6
7
8
9
10
11
12
# Define X and y
X = df[["leukocyte_count", "blood_pressure"]].values
y = df["tumor_class"].values

# Plot data
colors = {"benign": "red", "malignant": "blue"}
plt.scatter(X[:, 0], X[:, 1], c=[colors[_y] for _y in y], s=25, edgecolors="k")
plt.xlabel("leukocyte count")
plt.ylabel("blood pressure")
plt.legend(["malignant", "benign"], loc="upper right")
plt.show()

Split data

我们希望将数据集分成三份，使得每个子集中的类别分布相同，以便进行适当的训练和评估。

scikit-learn 提供的方法 train_test_split 可以很容易的做到。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
import collections
from sklearn.model_selection import train_test_split

TRAIN_SIZE = 0.7
VAL_SIZE = 0.15
TEST_SIZE = 0.15

def train_val_test_split(X, y, train_size):
    """Split dataset into data splits."""
    X_train, X_, y_train, y_ = train_test_split(X, y, train_size=TRAIN_SIZE, stratify=y)
    X_val, X_test, y_val, y_test = train_test_split(X_, y_, train_size=0.5, stratify=y_)
    return X_train, X_val, X_test, y_train, y_val, y_test

# Create data splits
X_train, X_val, X_test, y_train, y_val, y_test = train_val_test_split(
    X=X, y=y, train_size=TRAIN_SIZE)
print (f"X_train: {X_train.shape}, y_train: {y_train.shape}")
print (f"X_val: {X_val.shape}, y_val: {y_val.shape}")
print (f"X_test: {X_test.shape}, y_test: {y_test.shape}")
print (f"Sample point: {X_train[0]} → {y_train[0]}")

# Output
# X_train: (700, 2), y_train: (700,)
# X_val: (150, 2), y_val: (150,)
# X_test: (150, 2), y_test: (150,)
# Sample point: [18.60187909 18.37050035] → malignant

现在让我们看一下分割后的数据集中样本分布：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
# Overall class distribution
class_counts = dict(collections.Counter(y))
print (f"Classes: {class_counts}")
print (f'm:b = {class_counts["malignant"]/class_counts["benign"]:.2f}')

# Output
# Classes: {'malignant': 611, 'benign': 389}
# m:b = 1.57


# Per data split class distribution
train_class_counts = dict(collections.Counter(y_train))
val_class_counts = dict(collections.Counter(y_val))
test_class_counts = dict(collections.Counter(y_test))
print (f'train m:b = {train_class_counts["malignant"]/train_class_counts["benign"]:.2f}')
print (f'val m:b = {val_class_counts["malignant"]/val_class_counts["benign"]:.2f}')
print (f'test m:b = {test_class_counts["malignant"]/test_class_counts["benign"]:.2f}')

# Output
# train m:b = 1.57
# val m:b = 1.59
# test m:b = 1.54

可以看出，分割后的数据集里样本分布大体是接近的

Label encoding

注意到我们的分类标签是文本。我们需要将其进行编码，以便在模型中使用。

通常我们使用scikit-learn的LabelEncoder快速编码。

不过这里我们将编写自己的编码器，以便了解其具体的实现机制。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
import itertools


class LabelEncoder(object):
    """Label encoder for tag labels."""
    def __init__(self, class_to_index={}):
        self.class_to_index = class_to_index or {}  # mutable defaults ;)
        self.index_to_class = {v: k for k, v in self.class_to_index.items()}
        self.classes = list(self.class_to_index.keys())

    def __len__(self):
        return len(self.class_to_index)

    def __str__(self):
        return f"<LabelEncoder(num_classes={len(self)})>"

    def fit(self, y):
        classes = np.unique(y)
        for i, class_ in enumerate(classes):
            self.class_to_index[class_] = i
        self.index_to_class = {v: k for k, v in self.class_to_index.items()}
        self.classes = list(self.class_to_index.keys())
        return self

    def encode(self, y):
        encoded = np.zeros((len(y)), dtype=int)
        for i, item in enumerate(y):
            encoded[i] = self.class_to_index[item]
        return encoded

    def decode(self, y):
        classes = []
        for i, item in enumerate(y):
            classes.append(self.index_to_class[item])
        return classes

    def save(self, fp):
        with open(fp, "w") as fp:
            contents = {'class_to_index': self.class_to_index}
            json.dump(contents, fp, indent=4, sort_keys=False)

    @classmethod
    def load(cls, fp):
        with open(fp, "r") as fp:
            kwargs = json.load(fp=fp)
        return cls(**kwargs)


# Fit
label_encoder = LabelEncoder()
label_encoder.fit(y_train)
print (label_encoder.class_to_index)

# Output
# {'benign': 0, 'malignant': 1}


# Encoder
print (f"y_train[0]: {y_train[0]}")
y_train = label_encoder.encode(y_train)
y_val = label_encoder.encode(y_val)
y_test = label_encoder.encode(y_test)
print (f"y_train[0]: {y_train[0]}")
print (f"decoded: {label_encoder.decode([y_train[0]])}")

# Output
# y_train[0]: malignant
# y_train[0]: 1
# decoded: ['malignant']

我们还想计算出类别的权重，这对于在训练期间加权损失函数非常有用。它会告诉模型需要关注样本量不足的类别。

1
2
3
4
5
6
7
8
# Class weights
counts = np.bincount(y_train)
class_weights = {i: 1.0/count for i, count in enumerate(counts)}
print (f"counts: {counts}\nweights: {class_weights}")

# Output
# counts: [272 428]
# weight: {0: 0.003676470588235294, 1: 0.002336448598130841}

Standardize data

我们需要对数据进行标准化处理（零均值和单位方差），以便某个特定特征的大小不会影响模型学习其权重。

这里我们只需要标准化输入$X$，因为我们的输出$y$是离散标签，无须标准化。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
from sklearn.preprocessing import StandardScaler

# Standardize the data (mean=0, std=1) using training data
X_scaler = StandardScaler().fit(X_train)

# Apply scaler on training and test data (don't standardize outputs for classification)
X_train = X_scaler.transform(X_train)
X_val = X_scaler.transform(X_val)
X_test = X_scaler.transform(X_test)

# Check (means should be ~0 and std should be ~1)
print (f"X_test[0]: mean: {np.mean(X_test[:, 0], axis=0):.1f}, std: {np.std(X_test[:, 0], axis=0):.1f}")
print (f"X_test[1]: mean: {np.mean(X_test[:, 1], axis=0):.1f}, std: {np.std(X_test[:, 1], axis=0):.1f}")

# Output
# X_test[0]: mean: -0.0, std: 1.0
# X_test[1]: mean: 0.1, std: 1.0

Weights

我们的目标是学习一个逻辑回归模型 $\hat{y}$，用来建模自变量 $X$ 与 因变量 $y$ 的关系。

$$
\hat{y} = \frac{e^{W_yX}}{\sum_j{e^{WX}}}
$$

尽管我们的示例任务只涉及两个类别，但我们仍将使用多项式逻辑回归，因为softmax分类器可以推广到任意数量的类别。

第一步: 随机初始化模型的权重 $W$

1
2
3
4
5
6
7
8
9
10
11
12
INPUT_DIM = X_train.shape[1] # X is 2-dimensional
NUM_CLASSES = len(label_encoder.classes) # y has two possibilities (benign or malignant)

# Initialize random weights
W = 0.01 * np.random.randn(INPUT_DIM, NUM_CLASSES)
b = np.zeros((1, NUM_CLASSES))
print (f"W: {W.shape}")
print (f"b: {b.shape}")

# Output
# W: (2, 2)
# b: (1, 2)

Model

第二步 计算输入 $X$ 的对数值（$ z = WX $）。然后执行softmax操作得到预测类别的独热编码形式。

举个例子，如果有三个类别，那么一种可能的预测概率是[0.3, 0.3, 0.4]。
$$
\hat{y} = softmax(z) = softmax(WX) = \frac{e^{W_yX}}{\sum_j{e^{WX}}}
$$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
# Forward pass [NX2] · [2X2] + [1,2] = [NX2]
logits = np.dot(X_train, W) + b
print (f"logits: {logits.shape}")
print (f"sample: {logits[0]}")

# Output
# logits: (700, 2)
# sample: [0.0151033  0.03500428]


# Normalization via softmax to obtain class probabilities
exp_logits = np.exp(logits)
y_hat = exp_logits / np.sum(exp_logits, axis=1, keepdims=True)
print (f"y_hat: {y_hat.shape}")
print (f"sample: {y_hat[0]}")

# Output
# y_hat: (700, 2)
# sample: [0.49502492 0.50497508]

Loss

第三步 使用代价函数比较预测值 $\hat{y}$ （比如：[0.3, 0.3, 0.4]）和目标值 $y$ （比如：[0. 0. 1]）来确定损失 $J$。

逻辑回归的常见目标函数是交叉熵损失.

$$
J(\theta) = - \sum_i^K{log(\hat{y}_i)} = - \sum_i^K{log(\frac{e^{W_yX_i}}{\sum_j{e^{WX_i}}})}\\
$$

交叉熵损失函数的目标仍然是最小化预测与实际标签之间的差距，从而让模型能够更准确地进行分类.

1
2
3
4
5
6
7
# Loss
correct_class_logprobs = -np.log(y_hat[range(len(y_hat)), y_train])
loss = np.sum(correct_class_logprobs) / len(y_train)
print (f"loss: {loss:.2f}")

# Output
# 0.69

Gradients

第四步 计算损失函数 $J(\theta)$ 相对于权重的梯度。这里假设我们的类别是互斥的。
$$
\begin{split}
\frac{\partial{J}}{\partial{W_j}} &= \frac{\partial{J}}{\partial{\hat{y}}} \frac{\partial{\hat{y}}}{\partial{W_j}} = - \frac{1}{\hat{y}} \frac{\partial{\hat{y}}}{\partial{W_j}} \\
&= - \frac{1}{\frac{e^{W_yX}}{\sum_j{e^{WX}}}} \frac{\sum_j{e^{WX}e^{W_yX}0 - e^{W_yX}e^{W_jX}X}}{(\sum_j{e^{WX}})^2} = \frac{Xe^{W_jX}}{\sum_j{e^{WX}}} = X\hat{y}
\end{split}
$$

$$
\begin{split}
\frac{\partial{J}}{\partial{W_y}} &= \frac{\partial{J}}{\partial{\hat{y}}} \frac{\partial{\hat{y}}}{\partial{W_y}} = - \frac{1}{\hat{y}} \frac{\partial{\hat{y}}}{\partial{W_y}} \\
&= - \frac{1}{\frac{e^{W_yX}}{\sum_j{e^{WX}}}} \frac{\sum_j{e^{WX}e^{W_yX}X - e^{W_yX}e^{W_yX}X}}{(\sum_j{e^{WX}})^2} = \frac{1}{\hat{y}} (X\hat{y}^2 - X\hat{y}) = X(\hat{y} - 1)
\end{split}
$$

1
2
3
4
5
6

# Backpropagation
y_hat[range(len(y_hat)), y_train] -= 1
y_hat /= len(y_train)
dW = np.dot(X_train.T, y_hat)
db = np.sum(y_hat, axis=0, keepdims=True)

Update weights

第五步 指定一个学习率来更新权重 $W$，惩罚错误的分类奖励正确的分类。
$$
W_j = W_j - \alpha \frac{\partial{J}}{\partial{W_j}}
$$

1
2
3
4
5
LEARNING_RATE = 1e-1

# Update weights
W == -LEARNING_RATE * dW
b += -LEARNING_RATE * db

Training

第六步: 重复步骤 2 ~ 5，以最小化损失为目的来训练模型

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44

# Initialize random weights
W = 0.01 * np.random.randn(INPUT_DIM, NUM_CLASSES)
b = np.zeros((1, NUM_CLASSES))

# Training loop
NUM_EPOCHS = 50
LEARNING_RATE = 1e-1
for epoch_num in range(NUM_EPOCHS):

    # Forward pass [NX2] · [2X2] = [NX2]
    logits = np.dot(X_train, W) + b

    # Normalization via softmax to obtain class probabilities
    exp_logits = np.exp(logits)
    y_hat = exp_logits / np.sum(exp_logits, axis=1, keepdims=True)

    # Loss
    correct_class_logprobs = -np.log(y_hat[range(len(y_hat)), y_train])
    loss = np.sum(correct_class_logprobs) / len(y_train)

    # show progress
    if epoch_num%10 == 0:
        # Accuracy
        y_pred = np.argmax(logits, axis=1)
        accuracy =  np.mean(np.equal(y_train, y_pred))
        print (f"Epoch: {epoch_num}, loss: {loss:.3f}, accuracy: {accuracy:.3f}")

    # Backpropagation
    y_hat[range(len(y_hat)), y_train] -= 1
    y_hat /= len(y_train)
    dW = np.dot(X_train.T, y_hat)
    db = np.sum(y_hat, axis=0, keepdims=True)

    # Update weights
    W += -LEARNING_RATE * dW
    b += -LEARNING_RATE * db

# Output
# Epoch: 0, loss: 0.694, accuracy: 0.093
# Epoch: 10, loss: 0.451, accuracy: 0.973
# Epoch: 20, loss: 0.353, accuracy: 0.973
# Epoch: 30, loss: 0.299, accuracy: 0.973
# Epoch: 40, loss: 0.264, accuracy: 0.976

Evaluation

在测试集上评估我们训练好的模型。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class LogisticRegressionFromScratch():
    def predict(self, x):
        logits = np.dot(x, W) + b
        exp_logits = np.exp(logits)
        y_hat = exp_logits / np.sum(exp_logits, axis=1, keepdims=True)
        return y_hat


# Evaluation
model = LogisticRegressionFromScratch()
logits_train = model.predict(X_train)
pred_train = np.argmax(logits_train, axis=1)
logits_test = model.predict(X_test)
pred_test = np.argmax(logits_test, axis=1)


# Training and test accuracy
train_acc =  np.mean(np.equal(y_train, pred_train))
test_acc = np.mean(np.equal(y_test, pred_test))
print (f"train acc: {train_acc:.2f}, test acc: {test_acc:.2f}")

# Output
# train acc: 0.98, test acc: 0.97

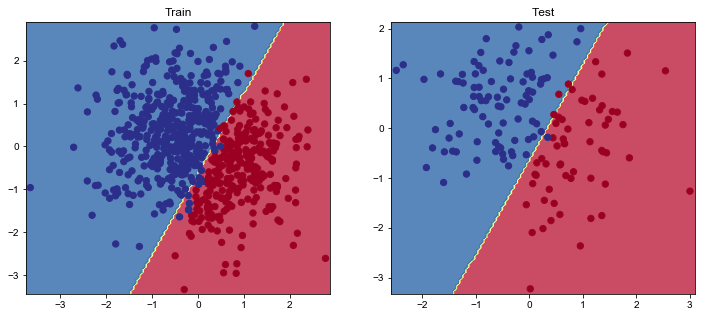
可视化我们的结果

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
def plot_multiclass_decision_boundary(model, X, y, savefig_fp=None):
    """Plot the multiclass decision boundary for a model that accepts 2D inputs.
    Credit: https://cs231n.github.io/neural-networks-case-study/

    Arguments:
        model {function} -- trained model with function model.predict(x_in).
        X {numpy.ndarray} -- 2D inputs with shape (N, 2).
        y {numpy.ndarray} -- 1D outputs with shape (N,).
    """
    # Axis boundaries
    x_min, x_max = X[:, 0].min() - 0.1, X[:, 0].max() + 0.1
    y_min, y_max = X[:, 1].min() - 0.1, X[:, 1].max() + 0.1
    xx, yy = np.meshgrid(np.linspace(x_min, x_max, 101),
                         np.linspace(y_min, y_max, 101))

    # Create predictions
    x_in = np.c_[xx.ravel(), yy.ravel()]
    y_pred = model.predict(x_in)
    y_pred = np.argmax(y_pred, axis=1).reshape(xx.shape)

    # Plot decision boundary
    plt.contourf(xx, yy, y_pred, cmap=plt.cm.Spectral, alpha=0.8)
    plt.scatter(X[:, 0], X[:, 1], c=y, s=40, cmap=plt.cm.RdYlBu)
    plt.xlim(xx.min(), xx.max())
    plt.ylim(yy.min(), yy.max())

    # Plot
    if savefig_fp:
        plt.savefig(savefig_fp, format="png")


# Visualize the decision boundary
plt.figure(figsize=(12,5))
plt.subplot(1, 2, 1)
plt.title("Train")
plot_multiclass_decision_boundary(model=model, X=X_train, y=y_train)
plt.subplot(1, 2, 2)
plt.title("Test")
plot_multiclass_decision_boundary(model=model, X=X_test, y=y_test)
plt.show()

Ending

可以看出，使用NumPy实现的代码相对复杂，下一篇我们即将看到PyTorch是如何便捷的实现逻辑回归。

Citation

1
2
3
4
5
6
@article{madewithml,
    author       = {Goku Mohandas},
    title        = { Logistic regression - Made With ML },
    howpublished = {\url{https://madewithml.com/}},
    year         = {2022}
}