TL;DR

Way2AI系列，确保出发去"改变世界"之前，我们已经打下了一个坚实的基础。

接上篇，本文的目标是使用PyTorch实现一个线性回归模型。

Generate data

我们复用上篇生成的数据。

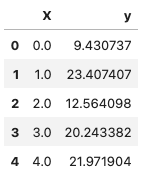
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt


SEED = 1024
NUM_SAMPLES = 50


# Generate synthetic data
def generate_data(num_samples):
    """Generate dummy data for linear regression."""
    X = np.array(range(num_samples))
    random_noise = np.random.uniform(-10, 20, size=num_samples)
    y = 3.5*X + random_noise # add some noise
    return X, y


# Generate random (linear) data
X, y = generate_data(num_samples=NUM_SAMPLES)
data = np.vstack([X, y]).T

# Load into a Pandas DataFrame
df = pd.DataFrame(data, columns=["X", "y"])
X = df[["X"]].values
y = df[["y"]].values

df.head()

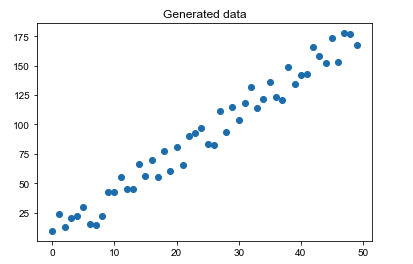
我们将数据绘制成散点图，可以看到它们有很明显的线性趋势。

1
2
3
4
# Scatter plot
plt.title("Generated data")
plt.scatter(x=df["X"], y=df["y"])
plt.show()

Split data

区别于上一篇中我们使用自定义摇骰子的方式分割数据，这里选择使用scikit-learn包里提供的train_test_split方法。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
from sklearn.model_selection import train_test_split

TRAIN_SIZE = 0.7
VAL_SIZE = 0.15
TEST_SIZE = 0.15

# Split (train)
X_train, X_, y_train, y_ = train_test_split(X, y, train_size=TRAIN_SIZE)

print (f"train: {len(X_train)} ({(len(X_train) / len(X)):.2f})\n"
       f"remaining: {len(X_)} ({(len(X_) / len(X)):.2f})")

# Output
# train: 35 (0.70)
# remaining: 15 (0.30)


# Split (test)
X_val, X_test, y_val, y_test = train_test_split(
    X_, y_, train_size=0.5)

print(f"train: {len(X_train)} ({len(X_train)/len(X):.2f})\n"
  f"val: {len(X_val)} ({len(X_val)/len(X):.2f})\n"
  f"test: {len(X_test)} ({len(X_test)/len(X):.2f})")

# Output
# train: 35 (0.70)
# val: 7 (0.14)
# test: 8 (0.16)

Standardize data

同样的，我们需要对数据进行标准化处理。这里使用scikit-learn里提供的StandardScaler。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
from sklearn.preprocessing import StandardScaler

# Standardize the data (mean=0, std=1) using training data
X_scaler = StandardScaler().fit(X_train)
y_scaler = StandardScaler().fit(y_train)

# Apply scaler on training and test data
X_train = X_scaler.transform(X_train)
y_train = y_scaler.transform(y_train).ravel().reshape(-1, 1)
X_val = X_scaler.transform(X_val)
y_val = y_scaler.transform(y_val).ravel().reshape(-1, 1)
X_test = X_scaler.transform(X_test)
y_test = y_scaler.transform(y_test).ravel().reshape(-1, 1)

# Check (means should be ~0 and std should be ~1)
print (f"mean: {np.mean(X_test, axis=0)[0]:.1f}, std: {np.std(X_test, axis=0)[0]:.1f}")
print (f"mean: {np.mean(y_test, axis=0)[0]:.1f}, std: {np.std(y_test, axis=0)[0]:.1f}")

# Output
# mean: 0.4, std: 1.0
# mean: 0.3, std: 0.9

Weights

我们将使用PyTorch的Linear layers来实现一个没有隐含层的神经网络。
关于神经网络我们后面会具体学习。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
import torch
from torch import nn

# Set seed for reproducibility
torch.manual_seed(SEED)

INPUT_DIM = X_train.shape[1] # X is 1-dimensional
OUTPUT_DIM = y_train.shape[1] # y is 1-dimensional

# Inputs
N = 3 # num samples
x = torch.randn(N, INPUT_DIM)
print (x.shape)
print (x.numpy())

# Output
# torch.Size([3, 1])
# [[-1.4836688 ]
#  [ 0.26714355]
#  [-1.8336787 ]]


# Weights
m = nn.Linear(INPUT_DIM, OUTPUT_DIM)
print (m)
print (f"weights ({m.weight.shape}): {m.weight[0][0]}")
print (f"bias ({m.bias.shape}): {m.bias[0]}")

# Output
# Linear(in_features=1, out_features=1, bias=True)
# weights (torch.Size([1, 1])): -0.2795013189315796
# bias (torch.Size([1])): -0.7643394470214844


# Forward pass
z = m(x)
print (z.shape)
print (z.detach().numpy())

# Output
# torch.Size([3, 1])
# [[-0.34965205]
#  [-0.8390064 ]
#  [-0.25182384]]

Model

$$
\hat{y} = WX + b
$$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class LinearRegression(nn.Module):
    def __init__(self, input_dim, output_dim):
        super(LinearRegression, self).__init__()
        self.fc1 = nn.Linear(input_dim, output_dim)

    def forward(self, x_in):
        y_pred = self.fc1(x_in)
        return y_pred


# Initialize model
model = LinearRegression(input_dim=INPUT_DIM, output_dim=OUTPUT_DIM)
print (model.named_parameters)

# Output
# <bound method Module.named_parameters of LinearRegression(
#   (fc1): Linear(in_features=1, out_features=1, bias=True)
# )>

Loss

同样的，我们使用PyTorch自带的Loss Functions, 这里指定MSELoss.

1
2
3
4
5
6
7
8
loss_fn = nn.MSELoss()
y_pred = torch.Tensor([0., 0., 1., 1.])
y_true =  torch.Tensor([1., 1., 1., 0.])
loss = loss_fn(y_pred, y_true)
print("Loss: ", loss.numpy())

# Output
# Loss:  0.75

Optimizer

上一篇中我们介绍了使用梯度下降的方法来更新我们的权重。PyTorch中有很多不同的权重更新方法，需要根据不同的场景来选择合适的。详见TORCH.OPTIM。
这里我们采用适合大多数场景的ADAM optimizer。

1
2
3
4
5
6
from torch.optim import Adam

LEARNING_RATE = 1e-1

# Optimizer
optimizer = Adam(model.parameters(), lr=LEARNING_RATE)

Training

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
# Convert data to tensors
X_train = torch.Tensor(X_train)
y_train = torch.Tensor(y_train)
X_val = torch.Tensor(X_val)
y_val = torch.Tensor(y_val)
X_test = torch.Tensor(X_test)
y_test = torch.Tensor(y_test)

# Training
NUM_EPOCHS = 100
for epoch in range(NUM_EPOCHS):
    # Forward pass
    y_pred = model(X_train)

    # Loss
    loss = loss_fn(y_pred, y_train)

    # Zero all gradients
    # https://stackoverflow.com/questions/48001598/why-do-we-need-to-call-zero-grad-in-pytorch
    optimizer.zero_grad()

    # Backward pass
    loss.backward()

    # Update weights
    optimizer.step()

    if epoch%20==0:
        print (f"Epoch: {epoch} | loss: {loss:.2f}")

# Output
# Epoch: 0 | loss: 1.11
# Epoch: 20 | loss: 0.10
# Epoch: 40 | loss: 0.04
# Epoch: 60 | loss: 0.03
# Epoch: 80 | loss: 0.03

Evaluation

现在我们准备评估我们训练好的模型。

1
2
3
4
5
6
7
8
9
10
11
12
13
# Predictions
pred_train = model(X_train)
pred_test = model(X_test)

# Performance
train_error = loss_fn(pred_train, y_train)
test_error = loss_fn(pred_test, y_test)
print(f"train_error: {train_error:.2f}")
print(f"test_error: {test_error:.2f}")

# Output
# train_error: 0.03
# test_error: 0.04

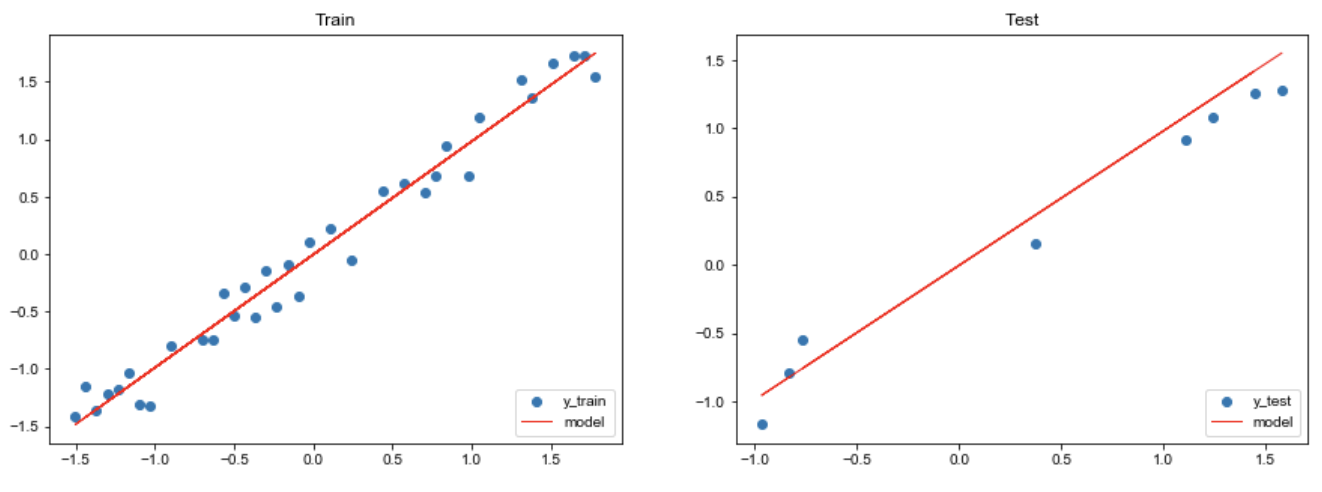
由于我们只有一个特征，因此可以轻松地对模型进行可视化。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
# Figure size
plt.figure(figsize=(15,5))

# Plot train data
plt.subplot(1, 2, 1)
plt.title("Train")
plt.scatter(X_train, y_train, label="y_train")
plt.plot(X_train, pred_train.detach().numpy(), color="red", linewidth=1, linestyle="-", label="model")
plt.legend(loc="lower right")

# Plot test data
plt.subplot(1, 2, 2)
plt.title("Test")
plt.scatter(X_test, y_test, label='y_test')
plt.plot(X_test, pred_test.detach().numpy(), color="red", linewidth=1, linestyle="-", label="model")
plt.legend(loc="lower right")

# Show plots
plt.show()

Inference

训练完模型后，我们可以使用它来对新数据进行预测。

1
2
3
4
# Feed in your own inputs
sample_indices = [10, 15, 25]
X_infer = np.array(sample_indices, dtype=np.float32)
X_infer = torch.Tensor(X_scaler.transform(X_infer.reshape(-1, 1)))

由于我们对数据都进行了标准化，所以对预测值需要进行逆操作。
$$
\hat{y}_{scaled} = \frac{\hat{y} - \mu_{\hat{y}}}{\sigma_{\hat{y}}}
$$

$$
\hat{y} = \hat{y}_{scaled} * \sigma_{\hat{y}} + \mu_{\hat{y}}
$$

1
2
3
4
5
6
7
8
9
10

# Unstandardize predictions
pred_infer = model(X_infer).detach().numpy() * np.sqrt(y_scaler.var_) + y_scaler.mean_
for i, index in enumerate(sample_indices):
    print (f"{df.iloc[index]['y']:.2f} (actual) → {pred_infer[i][0]:.2f} (predicted)")

# Output
# 28.10 (actual) → 40.99 (predicted)
# 56.45 (actual) → 58.62 (predicted)
# 100.83 (actual) → 93.88 (predicted)

Interpretability

线性回归具有高度可解释性的巨大优势。

1
2
3
4
5
6
7
8
9
10
11
# Unstandardize coefficients
W = model.fc1.weight.data.numpy()[0][0]
b = model.fc1.bias.data.numpy()[0]
W_unscaled = W * (y_scaler.scale_/X_scaler.scale_)
b_unscaled = b * y_scaler.scale_ + y_scaler.mean_ - np.sum(W_unscaled*X_scaler.mean_)
print ("[actual] y = 3.5X + noise")
print (f"[model] y_hat = {W_unscaled[0]:.1f}X + {b_unscaled[0]:.1f}")

# Output
# [actual] y = 3.5X + noise
# [model] y_hat = 3.5X + 5.7

Regularization

正则化有助于减少过拟合。本例使用L2正则化 (岭回归)。

通过L2正则化，我们对大的权重值进行惩罚，鼓励权重是较小值。 还有其他类型的正则化，比如L1（套索回归），它可以用于创建稀疏模型，其中一些特征系数被清零，或者结合了L1和L2惩罚的弹性正则化。

正则化不仅适用于线性回归，您可以使用它来处理任何模型的权重，包括我们将在未来学习到的模型。

$$
J(\theta) = \frac{1}{2} \sum_{i}(WX_i - y_i)^2 + \frac{\lambda}{2} \sum_i{W_i}^2
$$

$$
\frac{\partial(J)}{\partial(W)} = (\hat{y} - y)X + \lambda{W}
$$

$$
W = W - \alpha{\frac{\partial{J}}{\partial{W}}}
$$

$\lambda$: 正则化系数; $\alpha$: 学习率

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
L2_LAMBDA = 1e-2

# Initialize model
model = LinearRegression(input_dim=INPUT_DIM, output_dim=OUTPUT_DIM)

# Optimizer (w/ L2 regularization)
optimizer = Adam(model.parameters(), lr=LEARNING_RATE, weight_decay=L2_LAMBDA)

# Training
for epoch in range(NUM_EPOCHS):
    # Forward pass
    y_pred = model(X_train)

    # Loss
    loss = loss_fn(y_pred, y_train)

    # Zero all gradients
    optimizer.zero_grad()

    # Backward pass
    loss.backward()

    # Update weights
    optimizer.step()

    if epoch%20==0:
        print (f"Epoch: {epoch} | loss: {loss:.2f}")

# Output
# Epoch: 0 | loss: 0.67
# Epoch: 20 | loss: 0.06
# Epoch: 40 | loss: 0.03
# Epoch: 60 | loss: 0.03
# Epoch: 80 | loss: 0.03
1
2
3
4
5
6
7
8
9
10
11
12
13
# Predictions
pred_train = model(X_train)
pred_test = model(X_test)

# Performance
train_error = loss_fn(pred_train, y_train)
test_error = loss_fn(pred_test, y_test)
print(f"train_error: {train_error:.2f}")
print(f"test_error: {test_error:.2f}")

# Output
train_error: 0.03
test_error: 0.03

对于这个特定的例子，正则化并没有在性能上产生差异，因为我们的数据是从一个完美的线性方程生成的。但是对于大规模真实数据，正则化可以帮助我们的模型很好地泛化。

Ending

本篇基于上一篇的基础，简单介绍了如何用PyTorch实现线性回归。

Peace out.

Citation

1
2
3
4
5
6
@article{madewithml,
    author       = {Goku Mohandas},
    title        = { Linear regression - Made With ML },
    howpublished = {\url{https://madewithml.com/}},
    year         = {2022}
}