A Demo of the CNN LSTM

The moving square video prediction problem is contrived to demonstrate the CNN LSTM. The problem involves the generation of a sequence of frames. In each image a line is drawn from left to right or right to left. Each frame shows the extension of the line by one pixel. The task is for the model to classify whether the line moved left or right in the sequence of frames.Technically, the problem is a sequence classification problem framed with a many-to-one prediction model.

"Moving Square Video Prediction"是《Long Short-Term Memory Networks With Python》这本书里的一个示例。我在这里做了一下扩展，将其变成一个多分类问题。

The Problem

问题定义为一个帧序列，从边缘开始每多一帧就增加一个像素点，以展示朝某个方向延伸的一条线（从上到下，从下到上，从左到右，从右到左）。
模型的任务就是预测这条线是如何运动的。
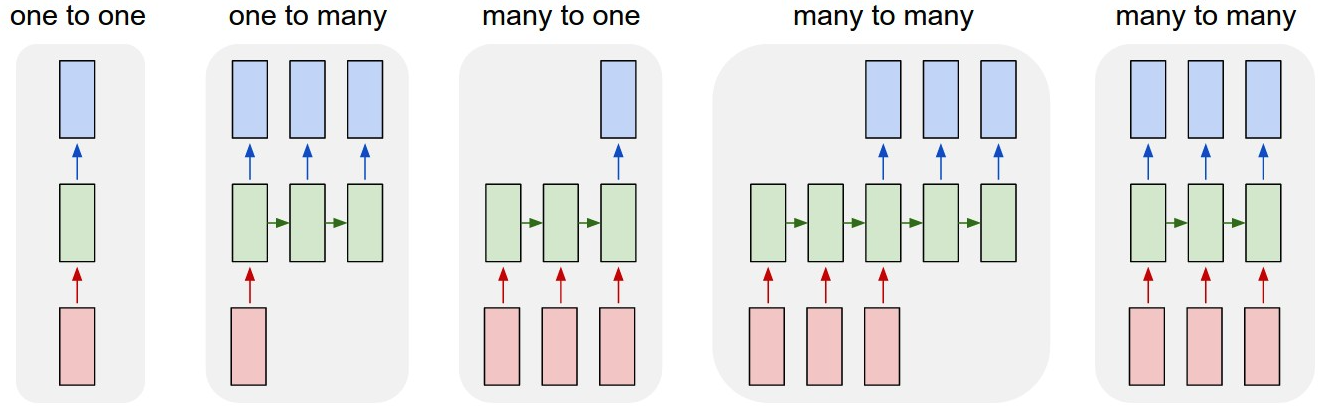
很明显，这就是一个many-to-one的分类任务。输入帧序列，输出单个标签（图片来源）。

Recurrent Neural Networks

# 代码示例
import numpy as np
from random import randint, random, choice

from matplotlib import pyplot

directions = ["Up", "Down", "Left", "Right"]


def next_frame(last_step, last_frame, row=None, col=None):
    lower = max(0, last_step-1)
    upper = min(last_frame.shape[0]-1, last_step+1)

    step = randint(lower, upper)

    frame = last_frame.copy()
    if row is not None:
        frame[row, step] = 1
    elif col is not None:
        frame[step, col] = 1
    return frame, step


def build_frames(size):
    frames = list()

    frame = np.zeros((size, size))
    step = randint(0, size-1)

    towards = choice(directions)
    if towards in ["Up", "Down"]:

        down = 1 if towards == "Down" else 0
        row = 0 if down else size-1
        frame[row, step] = 1
        frames.append(frame)

        for i in range(1, size):
            row = i if down else size-1-i
            frame, step = next_frame(step, frame, row=row)
            frames.append(frame)

    else:
        right = 1 if towards == "Right" else 0
        col = 0 if right else size-1
        frame[step, col] = 1
        frames.append(frame)

        for i in range(1, size):
            col = i if right else size-1-i
            frame, step = next_frame(step, frame, col=col)
            frames.append(frame)

    return frames, towards

size = 50

frames, towards = build_frames(size)

print(f"Towards: {towards}")

pyplot.figure(figsize=[8, 8])
for i in range(size):
    pyplot.subplot(size // 10, 10, i+1)
    pyplot.imshow(frames[i], cmap='Greys')
    ax = pyplot.gca()
    ax.get_xaxis().set_visible(False)
    ax.get_yaxis().set_visible(False)

pyplot.show()

显示运动方向为向上 (从左上到右下逐帧)

CNN LSTM

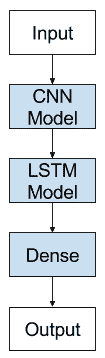
使用CNN层对输入数据进行特征提取, 使用LSTM来做序列预测。
这种架构还被用于语音识别和自然语言处理问题，其中CNN被用作音频和文本输入数据上的特征提取器，以供LSTM使用。
此架构适用于以下问题：

在其输入中具有空间结构，例如 2D 结构或图像中的像素或句子，段落或文档中的单词的一维结构。
在其输入中具有时间结构，诸如视频中的图像的顺序或文本中的单词，或者需要生成具有时间结构的输出，诸如文本描述中的单词。

卷积神经网络长短期记忆网络架构

generate_examples

from sklearn.preprocessing import LabelEncoder, OneHotEncoder


# label encode
label_encoder = LabelEncoder()
label_encoded = label_encoder.fit_transform(directions)
label_encoded = label_encoded.reshape(len(directions), 1)

# one hot encode
onehot_encoder = OneHotEncoder(sparse=False)
onehot_encoder.fit(label_encoded)

def generate_examples(size, n_patterns):
    X, y = list(), list()
    for _ in range(n_patterns):
        frames, towards = build_frames(size)
        X.append(frames)
        y.append(towards)
    X = np.array(X).reshape(n_patterns, size, size, size, 1)

    label_encoded = label_encoder.transform(np.array(y))
    y = onehot_encoder.transform(label_encoded.reshape(len(label_encoded), 1))
    return X, y

CNN Model

The Conv2D will interpret snapshots of the image (e.g. small squares) and the pooling layers will consolidate or abstract the interpretation.
We will define a Conv2D as an input layer with 2 filters and a 2 × 2 kernel to pass across the input images. The use of 2 filters was found with some experimentation and it is convention to use small kernel sizes. The Conv2D will output 2 49 × 49 pixel impressions of the input.

Convolutional layers are often immediately followed by a pooling layer. Here we use a MaxPooling2D pooling layer with a pool size of 2 × 2, which will in effect halve the size of each filter output from the previous layer, in turn outputting two 24 × 24 maps.

The pooling layer is followed by a Flatten layer to transform the [24,24,2] 3D output from the MaxPooling2D layer into a one-dimensional 1,152 element vector…

We want to apply the CNN model to each input image and pass on the output of each input image to the LSTM as a single time step.
We can achieve this by wrapping the entire CNN input model (one layer or more) in a TimeDistributed layer.

Next, we can define the LSTM elements of the model. We will use a single LSTM layer with 50 memory cells, configured after a little trial and error. The use of a TimeDistributed wrapper around the whole CNN model means that the LSTM will see 50 time steps, with each time step presenting a 1,152 element vector as input.


from keras.models import Sequential
from keras.layers import Conv2D
from keras.layers import MaxPooling2D
from keras.layers import LSTM
from keras.layers import Dense
from keras.layers import Flatten
from keras.layers import TimeDistributed

size = 50

# define the model
model = Sequential()
model.add(TimeDistributed(Conv2D(2, (2, 2), activation='relu'), input_shape=(None, size, size, 1)))
model.add(TimeDistributed(MaxPooling2D(pool_size=(2, 2))))
model.add(TimeDistributed(Flatten()))
model.add(LSTM(50))
model.add(Dense(len(directions), activation='softmax'))
model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['acc'])

model.summary()

Model Summary

fit and evaluate the model

# fit model
X, y = generate_examples(size, 5000)
model.fit(X, y, batch_size=32, epochs=1)

# evaluate model
X, y = generate_examples(size, 100)
loss, acc = model.evaluate(X, y, verbose=0)
print(f"loss: {loss:.10f} acc: {acc:.10f}")

fit & evaluate

prediction

# prediction on new data
for i in range(10):
    X, y = generate_examples(size, 1)

    yhat = model.predict(X, verbose=0)
    print(f"predict_i: {i}")
    print(label_encoder.inverse_transform([np.argmax(y[0, :])]), y)
    print(label_encoder.inverse_transform(np.array([np.argmax(yhat[0, :])])), yhat)

predictions

A Demo of the CNN LSTM

A Demo of the CNN LSTM

The Problem

CNN LSTM

generate_examples

CNN Model

fit and evaluate the model

prediction

Further Reading